4. ALT KÜME (KÜME PARÇASI)
a) Alt Küme
Herhangi iki A ve B kümeleri verilmiş olsun. A kümesinin her elemanı B
kümesinin de bir elemanı ise A kümesine B kümesinin bir alt kümesi denir. A ⊂ B
şeklinde yazılır “A alt küme B” diye okunur.
Bu tanıma göre, (A⊂ B) ⇔ (∀ x ∈ A⇒ x ∈ B) dir.
A ⊂ B yi şekildeki gibi Venn şeması ile gösterelim.
Venn şemasında B kümesi, A kümesini içine aldığından, B ⊃ A dır.
Bu da “B kapsar A” diye okunur.
A kümesinde olup B kümesinde olmayan en az bir eleman varsa, A kümesi B
kümesinin bir alt kümesi değildir. Bu durumda B kümesi A kümesini kapsamaz B ⊃ A
veya A ⊄ B fleklinde gösterilir.
ÖRNEK
A = {a, b, c, d, e} ve B = {a, c, e} kümeleri veriliyor. B kümesi, A kümesinin bir alt
kümesi olduğunu Venn şemasıyla gösterelim
Venn şemasında A ile B kümeleri gösterilmiştir. Burada B ⊂ A dır.
b. Alt Kümenin Özelikleri:
1. Etkisiz eleman özeliği: Boş küme, her kümenin bir alt kümesidir. (∅ ⊂ A)
2. Yansıma özeliği: Her küme, kendisinin bir alt kümesidir. (A ⊂ A)
3. Geçişme özeliği: A, B ve C kümeleri için, A kümesi B kümesinin alt kümesi ve B
kümesi de C kümesinin alt kümesi ise A kümesi C kümesinin bir alt kümesidir.
(A ⊂ B)Λ (B ⊂ C) ⇒ (A ⊂ C) (geçişme özeliği)
4. Ters simetri özeliği: A ve B kümeleri için, A kümesi B kümesinin alt kümesi ve
B kümesi de A kümesinin alt kümesi ise A kümesi B kümesine eşittir.
(A ⊂ B) Λ (B ⊂ A) ⇔ (A= B)
O halde, karşılıklı olarak birbirinin alt kümesi olan iki küme, birbirine eşittir
c. Alt Küme Sayısı
Verilen bir kümenin alt küme sayısınu bir örnekle açıklayalım.
Bu tanıma göre, (A⊂ B) ⇔ (∀ x ∈ A⇒ x ∈ B) dir.
A ⊂ B yi şekildeki gibi Venn şeması ile gösterelim.
Venn şemasında B kümesi, A kümesini içine aldığından, B ⊃ A dır.
Bu da “B kapsar A” diye okunur.
A kümesinde olup B kümesinde olmayan en az bir eleman varsa, A kümesi B
kümesinin bir alt kümesi değildir. Bu durumda B kümesi A kümesini kapsamaz B ⊃ A
veya A ⊄ B fleklinde gösterilir.
ÖRNEK
A = {a, b, c, d, e} ve B = {a, c, e} kümeleri veriliyor. B kümesi, A kümesinin bir alt
kümesi olduğunu Venn şemasıyla gösterelim
Venn şemasında A ile B kümeleri gösterilmiştir. Burada B ⊂ A dır.
b. Alt Kümenin Özelikleri:
1. Etkisiz eleman özeliği: Boş küme, her kümenin bir alt kümesidir. (∅ ⊂ A)
2. Yansıma özeliği: Her küme, kendisinin bir alt kümesidir. (A ⊂ A)
3. Geçişme özeliği: A, B ve C kümeleri için, A kümesi B kümesinin alt kümesi ve B
kümesi de C kümesinin alt kümesi ise A kümesi C kümesinin bir alt kümesidir.
(A ⊂ B)Λ (B ⊂ C) ⇒ (A ⊂ C) (geçişme özeliği)
4. Ters simetri özeliği: A ve B kümeleri için, A kümesi B kümesinin alt kümesi ve
B kümesi de A kümesinin alt kümesi ise A kümesi B kümesine eşittir.
(A ⊂ B) Λ (B ⊂ A) ⇔ (A= B)
O halde, karşılıklı olarak birbirinin alt kümesi olan iki küme, birbirine eşittir
c. Alt Küme Sayısı
Verilen bir kümenin alt küme sayısınu bir örnekle açıklayalım.
ÖRNEK
Verilen A = {1, 2, 3 } kümesinin eleman sayısı s (A) = 3 tür. Bu kümenin alt
kümelerini yazalım.
Boş küme (elemanı olmayan alt küme): ∅
Bir elemanlı alt kümeleri: {1 }, { 2}, { 3 }
iki elemanlı alt kümeleri: {1, 2} {1, 3}, {2, 3}
Üç elemanlı alt küme (Kümenin kendisi) : {1, 2, 3} dir.
A kümesinin bütün alt kümelerini yazarsak,
∅, {1 }, { 2}, { 3 }, {1, 2} {1, 3}, {2, 3}, {1, 2, 3} şeklindedir.
Böylece A kümesinin bütün alt kümelerin sayısı sekiz tane olur.
Eleman sayısı verilen alt küme sayısı
Bir kümenin alt kümelerinin sayısı bulunurken, kümenin eleman sayısı kadar 2 yan
yana yazılarak çarpılır.
ç. Özalt Küme
I. Özalt Küme
Bir kümenin eğer varsa kendisinden başka her alt kümesine, bu kümenin bir özalt
kümesi denir.
ÖRNEK
A = {a, b, c } kümesinin özalt kümelerini yazalım.
Tanıma göre, yazmamız gereken kümeler;
∅, {a}, {b}, {c}, {a, b}, {a, c}, (b, c} olur.
II. Özalt kümelerin sayısı
n elemanlı bir kümenin alt küme sayısı 2n dir. Her küme kendisinin alt kümesidir.
Kendinden başka her alt küme bir özalt küme olacağından, özalt kümelerinin sayısı
2n- 1 olur
d. n elemanlı bir kümenin r elemanlı alt küme sayısı
1. n elemanlı bir kümenin r elemanlı alt kümelerinden her birine, n nin r li
kombinasyonu denir. Buna göre, n elemanlı bir kümenin r elemanlı alt kümelerinin sayısı ;
olur.
ÖRNEK
Beş elemanlı bir A kümesinin, üç tane elemanı olan alt kümelerinin sayısını bulalım.
tanedir.
ÖRNEK
Altı tane elemanı olan bir A kümesinin , en az üç elemanı olan alt kümelerinin sayısının
bulalım.
I. Yol: Altı elemanlı bir kümenin en az üç elemanlı alt küme sayısı,
II. Yol
ÖRNEK
A = {1, 3, 5, 7, 9} kümesi veriliyor. Bu kümenin en çok iki elemanlı alt küme
sayısını bulalım.
A = { 1, 3, 5, 7, 9 } olduğundan s (A) = 5 tir. Buna göre, en çok iki elemanlı alt
küme sayısı ,
e. Kuvvet kümesi
A herhangi bir küme olmak üzere, A kümesinin bütün alt kümelerinin kümesine, A
kümesinin kuvvet kümesi denir. Kuvvet kümesi P(A) ile gösterilir.
n elemanlı bir A kümesinin kuvvet kümesinin eleman sayısı 2n dir.
s [p(A)] = 2n olur.
ÖRNEK
A = {3, 5, 7} kümesi veriliyor. A kümesinin kuvvet kümesini yazalım. Kuvvet
kümesinin eleman sayısını bulalım
Verilen A kümesinin bütün alt kümelerini yazarsak,
P(A) = {∅, {3}, {5}, {7}, {3, 5}, {3, 7}, {5, 7}, {3, 5, 7}olur.
Böylece A kümesinin kuvvet kümesini yazmış oluruz
A kümesinin eleman sayısı n = 3 olduğundan, s[p(A)] = 2n ifadesinden, 23 = 8 dir.
O halde, A kümesinde kuvvet kümesinin eleman sayısı 8 olur
ÖRNEK
Beş elemanlı bir A kümesinin, üç tane elemanı olan alt kümelerinin sayısını bulalım.
tanedir.
ÖRNEK
Altı tane elemanı olan bir A kümesinin , en az üç elemanı olan alt kümelerinin sayısının
bulalım.
I. Yol: Altı elemanlı bir kümenin en az üç elemanlı alt küme sayısı,
II. Yol
ÖRNEK
A = {1, 3, 5, 7, 9} kümesi veriliyor. Bu kümenin en çok iki elemanlı alt küme
sayısını bulalım.
A = { 1, 3, 5, 7, 9 } olduğundan s (A) = 5 tir. Buna göre, en çok iki elemanlı alt
küme sayısı ,
e. Kuvvet kümesi
A herhangi bir küme olmak üzere, A kümesinin bütün alt kümelerinin kümesine, A
kümesinin kuvvet kümesi denir. Kuvvet kümesi P(A) ile gösterilir.
n elemanlı bir A kümesinin kuvvet kümesinin eleman sayısı 2n dir.
s [p(A)] = 2n olur.
ÖRNEK
A = {3, 5, 7} kümesi veriliyor. A kümesinin kuvvet kümesini yazalım. Kuvvet
kümesinin eleman sayısını bulalım
Verilen A kümesinin bütün alt kümelerini yazarsak,
P(A) = {∅, {3}, {5}, {7}, {3, 5}, {3, 7}, {5, 7}, {3, 5, 7}olur.
Böylece A kümesinin kuvvet kümesini yazmış oluruz
A kümesinin eleman sayısı n = 3 olduğundan, s[p(A)] = 2n ifadesinden, 23 = 8 dir.
O halde, A kümesinde kuvvet kümesinin eleman sayısı 8 olur


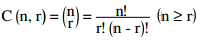


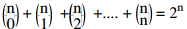




Kümeler – Konu Anlatımı ve Soru Çözümü
YanıtlaSilEğitim hayatımızın ilk yıllarından beri karşımıza çıkan, temelden oldukça basit ve sık sık kullandığımız fakat teoride ince detayları olan tyt matematik kümeler konu anlatımı içeriğimizle sizlerleyiz. YKSDestek.com ekibi olarak şu ana kadar ilk oturumda karşımıza çıkabilecek matematik konuları hakkında detaylar verdik. Bunlara sitemiz üzerinden ulaşabilirsiniz. Konu anlatımının yanı sıra tyt matematik kümeler soru çözümü için...
kümeler soru çözümü